正交投影变换

2021-06-232022-05-05753

正交投影变换

在webgl里，我们观察物体，只有物体在可视范围内才会被绘制，可视范围一般有长方体和锥形的，长方体可视空间是由正交投影产生的，另外一个是金字塔塔型的，具有近大远小的效果。正交投影变换不涉及到近大远小这种问题，还是比较简单的。只有一个坐标的转换，在使用正交投影的时候，基本上是将物体投影到一个规范化的立体空间里。如下图（百度图片找的）

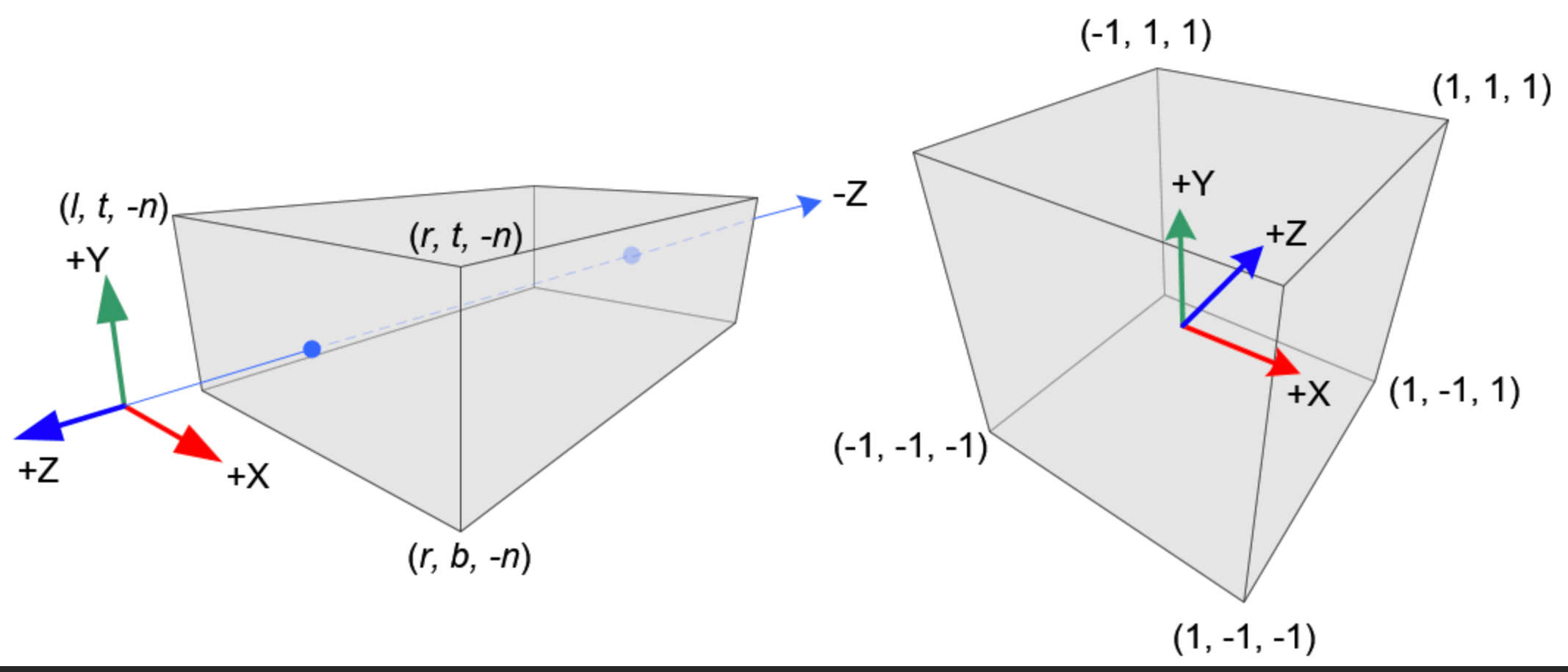
image-20210208175930365

正交投影变换的计算

假设webgl上显示的一点(ox,oy,oz)(o_x,o_y,o_z)， 投影到投影空间的点是(px,py,pz)(p_x, p_y, p_z)，

  • t 近裁剪平面上面那条边
  • b 近裁剪平面下面那条边
  • l,r对应左右边

webgl的x轴坐标范围在[-1, 1]之间，投影空间里的点的范围是[l, r]，如果需要将物体上的点转化到这个范围里面，根据线性映射的话可以得出一个式子

px−(−1)1−(−1)=ox−lr−l\frac{p_x - (-1)}{1 - (-1)} = \frac{o_x - l}{r - l} 可以变换得到 px=2r−lox−r+lr−lp_x = \frac{2}{r-l}o_x - \frac{r + l}{r - l}

同理 py=2t−boy−t+bt−bp_y = \frac{2}{t-b}o_y - \frac{t + b}{t - b}

pz=2f−noz−f+nf−np_z = \frac{2}{f-n}o_z - \frac{f + n}{f - n}

将三个式子写成矩阵的话

p=[2r−l00−r+lr−l02t−b0−t+bt−b00−2f−n−f+nf−n0001]⋅[ox,oy,oz,1]p = \begin{bmatrix} \frac{2}{r-l} & 0 & 0 & -\frac{r + l}{r-l}\\0 & \frac{2}{t-b} & 0 & -\frac{t + b}{t-b} \\ 0 & 0 &\frac{-2}{f-n} & -\frac{f + n}{f-n} \\ 0 & 0 &0& 1\end{bmatrix} \cdot [o_x, o_y, o_z, 1]

这样我们就得到了正交投影变换矩阵

个人理解的补充(不一定正确，但是我觉得能解释我的疑惑)

正交投影矩阵变换和透视投影矩阵变换本身并不进行将物体从三维空间投影到二维空间操作，只是进行了投影的前置操作。webgl本身是有一个可视空间的，是[-1,1]范围的长宽为2长方体，在这个范围内的物体会被投影到2d的屏幕，由webgl操作。我们需要做的就是将我们定义物体的坐标按需求映射到这个webgl自带的可视空间里。所以正交投影只是进行了坐标的缩放，从我们自己定义的可视空间的坐标转换到webgl的[-1,1]里，这样转换的时候z轴是个计算的式子，而不是固定的值。

参考文章

http://www.manew.com/thread-108023-1-1.html